Gazdag Géza csengő-problémája

Az előző részben ezt megoldottad, ugye? Valami ilyesmi kapcsolási rajz jött ki?

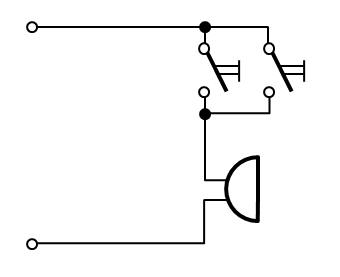
Két gombos csengő kapcsrajz

Nincs ebben semmi mágia, kérem szépen! Jön a villany, és bármelyik megnyomott gombon keresztül tud menni, nem? Persze ha mindkettőt megnyomod, akkor mindkettőt használja a villany.

A csengő akkor szól, ha megnyomják az egyik gombot, VAGY ha megnyomják a másik gombot. (Meg akkor is, ha mindkettőt.)

Brit tudósok megmondják, hogyan gondolkodunk

Ekkor ugyan Anglia volt a neve az országnak, ahol George Boole kiadott egy érdekes művet: A gondolkodás törvényeit.

1854-ben járunk, a sötét informatikai őskorban, ami szó szerint sötét volt, mert az izzólámpát sem találták még fel ekkor. Mégis, ez a bácsi, aki matematika professzor volt, elkezdte fejtegetni, hogy hogyan lehetne leírni a gondolkodás, a döntés folyamatát úgy, hogy annyira egyértelmű legyen, mint két szám összeadása.

Mert hiszen a hagyományos számtan már 4000 éves, és minden nap használja az ember dolgok megszámlálására, vagy éppen kiszámolására. De ez nem alkalmas arra, hogy döntéseket írjunk le vele, nincs olyan számtani formula, amivel le lehet írni, hogy "amennyiben szép az idő, és ráérek, akkor lemegyek a térre".

Hagyományos algebra

Szimbólumok:

• valamiből semennyi sincs (0)
• valamiből egy darab van (1)
• valamiből kettő darab van (2)
• valamiből három darab van (3)
• valamiből négy darab van (4)
• valamiből öt darab van (5)
• valamiből hat darab van (6)
• valamiből hét darab van (7)
• valamiből nyolc darab van (8)
• valamiből kilenc darab van (9)
• valamiből több van: helyiértékes ábrázolás, pld. ha kilencvenegy van akkor az (91)

Műveletek:

• összeadás (+)
• kivonás (-)
• szorzás (·)
• osztás (/)

Tipikus célok:

• ha van 4 csirkém és veszek még 3 csirkét, hány csirkém van?

x=4+3

• mennyi lába van 8 csirkének?

x=8·2

Boole algebra

Boole bevezetett egy új matekot. Más szimbólumok, más műveletek, más célok leírására.

Szimbólumok:

• hamis, vagy nem, vagy nincs (0)
• igaz, vagy igen, vagy van (1)

Műveletek:

• invertálás (felülvonás), vagy (-) esetleg (¬) néhol (˜), szövegesen NOT
• és (·) esetleg (&), szövegesen AND
• vagy (+) esetleg (|), szövegesen OR
• kizáró-vagy (⊕), szövegesen XOR

Tipikus célok:

• Ha szép az idő, akkor érdemes lemenni a térre. Ha van időm, lemehetek a térre. Mikor mehetek a térre?

lemegyek=szépidő AND vanidőm

• Van egy százasom, amit bedobhatok az automatába. Ezért vagy kávét, vagy teát tudok kapni (mindkettőt nem). Kapok-e italt, ha megnyomom a tea vagy a kávé gombokat? Ha egyiket sem? Ha mindkettőt?

ital=kávégomb XOR teagomb

Mire jó a Boole algebra?

Eddig ez csak merő agymenés, nem? Viszont egy dolgot már sejtesz: Boole műveleteket - vagy ahogy mások nevezik, logikai műveleteket - nagyon jól tudsz csinálni villannyal!

Nem hiszed? Na ezt figyeld. Például, a hűtőlámpa akkor kapcsolódjon be, amikor a gomb nincs bekapcsolva. A láncfűrész akkor kapcsolódjon be, ha az egyik gomb és a másik gomb is be van kapcsolva. Kapizsgálod?

hűtőlámpa = NOT gomb

motor = gomb1 AND gomb2

csengő = gomb1 OR gomb2

Ezek a cuccaink logikai kifejezésekkel írhatók le. Sőt, úgy is mondhatjuk, hogy ezek a cuccaink kiszámolják a logikai kifejezések értékét.